Digite uma palavra ou frase em qualquer idioma 👆
Idioma:
Tradução e análise de palavras por inteligência artificial ChatGPT
Nesta página você pode obter uma análise detalhada de uma palavra ou frase, produzida usando a melhor tecnologia de inteligência artificial até o momento:
- como a palavra é usada
- frequência de uso
- é usado com mais frequência na fala oral ou escrita
- opções de tradução de palavras
- exemplos de uso (várias frases com tradução)
- etimologia
чрезвычайная мера - tradução para Inglês
СТРАНИЦА ЗНАЧЕНИЙ В ПРОЕКТЕ ВИКИМЕДИА
Мера вероятности; Мера (река)
чрезвычайная мера
мера
extraordinary measures
общая лексика
чрезвычайные меры
Definição
Мера множества
математическое понятие, обобщающее понятия длины отрезка, площади плоской фигуры и объёма тела на множества более общей природы. В качестве примера можно привести определение меры Лебега (введённой А. Лебегом в 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения. При этом и способ сравнения напоминает обычный процесс измерения площади. Меру Лебега m (Δ) любого квадрата Δ полагают равной его площади. Затем рассматриваемое множество А покрывают конечным или бесконечным числом квадратов Δ1, Δ2,..., Δn,...; нижнюю грань чисел
взятую по всевозможным покрытиям множества А, называют верхней (внешней) мерой m*(А) множества А. Нижняя (внутренняя) мера m* (А) множества А определяется как разность
где Δ - какой-либо квадрат, содержащий множество А, и  - множество всех точек этого квадрата, не содержащихся в А. Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m (А) верхней и нижней мер - мерой Лебега множества А. Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область), измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.
- множество всех точек этого квадрата, не содержащихся в А. Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m (А) верхней и нижней мер - мерой Лебега множества А. Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область), измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.
Основные свойства меры Лебега: 1) мера любого множества неотрицательна: m (A)Δ ́≥ ́0; 2) мера суммы
конечной или счётной системы попарно непересекающихся множеств A1, A2..., An... равна сумме их мер:
3) при перемещении множества как твёрдого тела его мера не меняется.
Своеобразие понятия "М. м." можно пояснить следующим примером: множество А рациональных точек интервала (0, 1) и множество В иррациональных точек того же интервала сходны в том смысле, что каждое из них плотно на интервале (0, 1), т. е., что между любыми двумя точками указанного интервала найдутся как точки множества А, так и точки множества В; в то же время они резко различаются по мере: m (А) = 0, а m (В) = 1.
Для более узких классов множеств мера, совпадающая с лебеговской, была ранее определена М. Э. К. Жорданом (1893) и Э. Борелем (См. Борель) (1898). О других вопросах, связанных с мерой Лебега, см. Интеграл.
Развитие ряда отделов современной математики привело к дальнейшим обобщениям - созданию т. н. абстрактной теории меры. При этом М. м. определяют аксиоматически. Пусть U - произвольное множество и 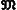 - некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в
- некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в  , называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в
, называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в  , сумма А которых входит в
, сумма А которых входит в  , имеет место равенство
, имеет место равенство
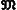 - некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в
- некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в  , называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в
, называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в  , сумма А которых входит в
, сумма А которых входит в  , имеет место равенство
, имеет место равенство и если, кроме того, система  удовлетворяет определённым дополнительным условиям. Множества, входящие в
удовлетворяет определённым дополнительным условиям. Множества, входящие в  , называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования.
, называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования.
 удовлетворяет определённым дополнительным условиям. Множества, входящие в
удовлетворяет определённым дополнительным условиям. Множества, входящие в  , называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования.
, называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования. Многие основные утверждения из теории меры Лебега, теории измеримых функций и интеграла Лебега сохраняются с соответствующими видоизменениями и в абстрактной теории меры и интеграла. Последняя составляет математическое основание современной теории вероятностей, данное в 1933 А. Н. Колмогоровым. Специальный интерес для ряда областей математики представляют меры, инвариантные по отношению к той или иной группе преобразований множества U в себя.
Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М. - Л., 1934; Сакс С., Теория интеграла, пер. с англ., М., 1949; Халмош П. Р., Теория меры, пер. с англ., М., 1953.
Ю. В. Прохоров.
Exemplos do corpo de texto para чрезвычайная мера
1. Объяснялась эта чрезвычайная мера тем, что Зеленовы якобы начали запугивать свидетелей.
2. Чрезвычайная мера была принята для того, чтобы предотвратить исчезновение этой ценной рыбы семейства осетровых.
3. "Чрезвычайная мера" Бертольта Брехта из норвежского Бергена (Транзиттеатр) уже засветилась в самой Скандинавии.
4. Как пояснили в Газпроме, эта чрезвычайная мера вызвана аномально холодной российской погодой...
5. Это чрезвычайная мера, но именно таких мер до сих пор придерживались богатые страны.

